Maker of the Optical Design Software OpTaliX

Home  | Download  | Prices  | About Us  | Sign-In  | FAQ  | Links

Optimization

Optimization of an optical system requires the solution of a highly nonlinear problem. It is the process by which the aberrations of a lens are minimized by changing selected lens data (variables). Two types of optimization algorithms are available;

KT - optimization, minimizes an error function by a damped-least-square (DLS) method subject to solving constraints using Lagrange multipliers and application of the Kuhn-Tucker optimality condition,
LM - optimization, solves a problem using a modified Levenberg-Marquardt algorithm.


The merit function is constructed from almost any command relating to performance or construction data, thus allowing unlimited flexibility in the definition of the error function (also called a merit function). Besides minimization, boundary constraints accept logical operators like

  =   (equal),
  <   (less than)
  >   (greater than).


User-defined variables and functions will allow an even broader range of constraints in optimization, for example,

$z = [efl]+23.12
@xyz == [thi s2]+[thi s4]+$z
@xyz > 10



Defining Optimization Variables, Targets and Constraints



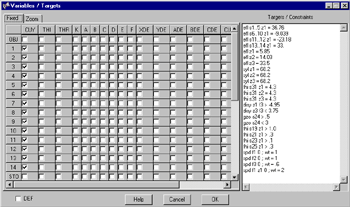
Edit variables, targets and constraints comfortably in a single window. The definition of a user merit function accepts all commands relating to surface data, system data and performance data. This includes arithmetic expressions, a large number of built-in mathematical functions and lens database items as also shown in the macro examples. See below a few examples of defining merit function elements:

efl = 100 Focal length (EFL) shall be precisely 100 mm.
syl < 70 Constrain system length (first surface to last surface) to less than 70 mm.
spd f1..3 w3..4 0 Minimize rms-spot diameter (spd) at field points 1 to 3 and wavelength numbers 3 to 4 (Target is 0).
spd 0 As above, minimize rms-spot diameter. Absence of field and wavelength qualifier implies all fields and wavelengths. This is one of the easiest yet powerful optimization target.
thi s1 = [OAL] - 2*[thi s4] Use arithmetic operators and lens database items given in [ ] brackets to define complex targets.
bfl = sqrt(tan(2)) Use intrinsic functions to define complex targets.
@myfkn == [oal s1..6]-5.0 Construct a user-defined function to be used later.
@myfkn > 10 Use a previously defined funtion to define a constraint in optimization.